Objetivo: El alumno comprenderá el concepto de integral definida así como su
interpretación gráfica. Resolverá problemas de aplicación geométrica al mismo
tiempo que resolverá problemas del entorno económico-administrativo.
El alumno aplicará técnicas adicionales para la resolución de integrales
que presentan estructuras complejas asociadas con modelos y problemas del
entorno económico-administrativo.
El
alumno entenderá los conceptos elementales del álgebra lineal y los aplicará en
problemas del ámbito económico y de gestión de negocios.
3.1 Área Bajo la Curva
Área Bajo una Curva
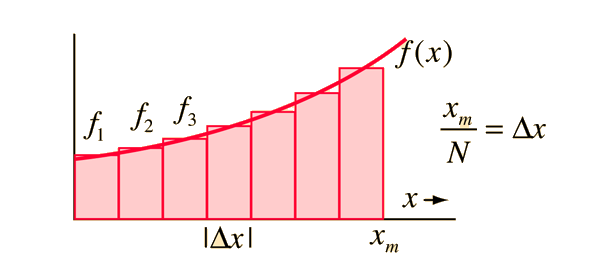
La formulación del área bajo una curva es el primer paso para desarrollar el concepto de integral. El área bajo la curva formada por el trazo de la función f(x) y el eje x se puede obtener aproximadamente, dibujando rectángulos de anchura finita y altura f igual al valor de la función en el centro del intervalo.

Si hacemos mas pequeño la anchura del rectángulo, entonces el número N es mas grande y mejor la aproximación al valor del área.
Autor: hyperphysics
3.2 Teorema Fundamental del Cálculo
El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función acotada e integrable (siendo continua o discontinua en un número finito de puntos) verifica que la derivada de su integral es igual a ella misma. Este teorema es central en la rama de las matemáticas denominada análisis matemático o cálculo.
El teorema es fundamental porque hasta entonces el cálculo aproximado de áreas -integrales- en el que se venía trabajando desde Arquímedes, era una rama de las matemáticas que se seguía por separado al cálculo diferencial que se venía desarrollando por Isaac Newton, Isaac Barrow y Gottfried Leibniz en el siglo XVIII y dio lugar a conceptos como el de las derivadas. Las integrales eran investigadas como formas de estudiar áreas y volúmenes, hasta que en ese punto de la historia ambas ramas convergieron, al demostrarse que el estudio del "área bajo una función" estaba íntimamente vinculado al cálculo diferencial, resultando la integración, la operación inversa a la derivación.
Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la integral indefinida de la función al ser integrada.
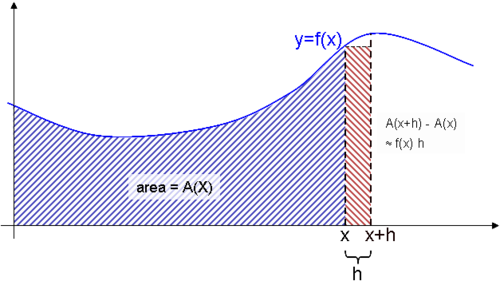
Su póngase que se tiene una función continua y = f(x) y que su representación gráfica es una curva. Entonces, para cada valor de x tiene sentido de manera intuitiva pensar que existe una función A(x) que representa el área bajo la curva entre 0 y x aún sin conocer su expresión.
Su póngase ahora que se quiere calcular el área bajo la curva entre x yx+h. Se podría hacer hallando el área entre 0 y x+h y luego restando el área entre 0 y x. En resumen, el área de esta especie de "loncha" sería A(x+h) −A(x).
Otra manera de estimar esta misma área es multiplicar h por f(x) para hallar el área de un rectángulo que coincide aproximadamente con la "loncha". Nótese que la aproximación al área buscada es más precisa cuanto más pequeño sea el valor de h.
Por lo tanto, se puede decir que A(x+h) − A(x) es aproximadamente igual a f(x) · h, y que la precisión de esta aproximación mejora al disminuir el valor de h. En otras palabras, ƒ(x)·h ≈ A(x+h) − A(x), convirtiéndose esta aproximación en igualdad cuando h tiende a 0 como límite.
Dividiendo los dos lados de la ecuación por h se obtiene
Cuando h tiende a 0, se observa que el miembro derecho de la ecuación es sencillamente la derivada A’(x) de la función A(x) y que el miembro izquierdo se queda en ƒ(x) al ya no estar h presente.
Se muestra entonces de manera informal que ƒ(x) = A’(x), es decir, que la derivada de la función de área A(x) es en realidad la función ƒ(x). Dicho de otra forma, la función de área A(x) es la antiderivada de la función original.
Lo que se ha mostrado es que, intuitivamente, calcular la derivada de una función y "hallar el área" bajo su curva son operaciones "inversas", es decir el objetivo del teorema fundamental del cálculo integral.
|
Usando la Regla de la cadena obtenemos como consecuencia directa del primer teorema fundamental del cálculo infinitesimal:
Siendo f(t) una función integrable sobre el intervalo [a(x),b(x)] con a(x) y b(x) derivables.
Lema
Sea  integrable sobre
integrable sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y
y
 integrable sobre
integrable sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y
y
Entonces
Está claro que 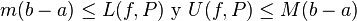 para toda partición
para toda partición  . Puesto que
. Puesto que  , la desigualdad se sigue inmediatamente.
, la desigualdad se sigue inmediatamente.
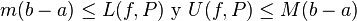 para toda partición
para toda partición 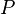 . Puesto que
. Puesto que  , la desigualdad se sigue inmediatamente.
, la desigualdad se sigue inmediatamente.
Por definición se tiene que  .
.
 .
.
Sea h>0. Entonces 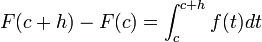 .
.
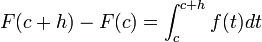 .
.
Se define 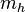 y
y 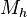 como:
como:
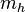 y
y 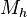 como:
como:-
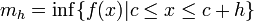 ,
,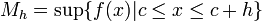
Aplicando el 'lema' se observa que
-
 .
.
Por lo tanto,
Sea 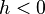 . Sean
. Sean
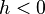 . Sean
. Sean-
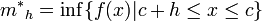 ,
,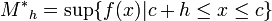 .
.
Aplicando el 'lema' se observa que
-
 .
.
Como
-
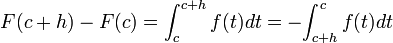 ,
,
entonces,
-
 .
.
Puesto que 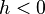 , se tiene que
, se tiene que
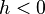 , se tiene que
, se tiene que-
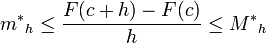 .
.
Y como  es continua en c se tiene que
es continua en c se tiene que
 es continua en c se tiene que
es continua en c se tiene que-
 ,
,
y esto lleva a que
-
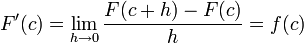 .
.
Cogiendo un intervalo cerrado ![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) sobre
sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ya que
, ya que  es continua en
es continua en ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , también lo será en
, también lo será en ![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) .
.
![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) sobre
sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ya que
, ya que  es continua en
es continua en ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , también lo será en
, también lo será en ![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) .
.
Según el teorema del valor medio para integrales se cumple que:
Haciendo el intervalo muy pequeño de tal manera que  y debido a esa tendencia se tiene también que
y debido a esa tendencia se tiene también que 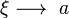
 y debido a esa tendencia se tiene también que
y debido a esa tendencia se tiene también que 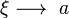
Por lo que en los límites se llega a:
Sabemos que :

Entonces la ecuación se la puede escribir como :
Dado que 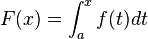 , entonces
, entonces 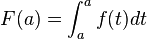
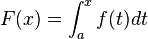 , entonces
, entonces 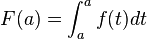
Y debido a que  es continua en a, entonces
es continua en a, entonces 
 es continua en a, entonces
es continua en a, entonces 
Vista la ecuación de otra manera:
Por lo tanto
O también
Y en consecuencia
Con ello se demuestra el primer teorema fundamental del cálculo.
El segundo teorema fundamental del cálculo integral (o regla de Newton-Leibniz, o también regla de Barrow, en honor al matemático inglés Isaac Barrow, profesor de Isaac Newton) es una propiedad de las funciones continuas que permite calcular fácilmente el valor de la integral definida a partir de cualquiera de las primitivas de la función.
|
Considere la siguiente primitiva de  definida en el intervalo
definida en el intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .:
.:
 definida en el intervalo
definida en el intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .:
.:-
-
 .
.
-
esto debido al primer teorema fundamental del cálculo el cual establece que:
-
-
![G'(x)=f(x) {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/c/1/c/c1c5b14eec3a07078372ecbb92a559e5.png) .
.
-
Como  y
y  son primitivas de
son primitivas de  , entonces
, entonces
 y
y  son primitivas de
son primitivas de  , entonces
, entonces-
-
![\exists C \in \mathbb{R}: {\ }G(x)=F(x)+C, {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/b/7/7/b7724a98dad3e4e2b5116f519cf5708c.png) .
.
-
Observe que
y de eso se sigue que 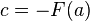 ; por lo tanto,
; por lo tanto,
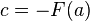 ; por lo tanto,
; por lo tanto,-
-
 .
.
-
Y en particular si 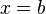 :
:
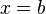 :
:
Como se puede integrar inmediatamente.
Autor: Wikipedia
3.3 Propiedades de la Integral Definida
Autor: Vitutor
3.4 Área Entre Una y Dos Curvas
Autor: Inetor
3.5
Aplicaciones: Excedente del Consumidor y del Productor, Valor Presente y Valor Futuro
Excedente del consumidor
Podemos definir el excedente del consumidor como la diferencia entre el precio máximo que estaría dispuesto a pagar y el precio que realmente paga. Consideremos la siguiente curva de demanda de un individuo, si el precio de mercado es pE demandara qE. No obstante, por la primera unidad hubiera estado dispuesto a pagar mucho más p1 , por la segunda unidad algo menos que por la primera pero más de lo que realmente paga, y así sucesivamente hasta la cantidad qE en donde coincide el precio que paga y el que está dispuesto a pagar. Gráficamente, la zona que muestra la divergencia entre la disposición marginal a pagar y el precio satisfecho reflejaría el excedente del consumidor.
Excedente del productor
Para estimar el excedente del productor deberemos de partir de la función de oferta. Dado un precio en el mercado pE, compararemos el precio al que estarían dispuesto a ofrecer cada unidad de mercancía con el precio que realmente perciben. Y observaremos que hasta qE el empresario por cada unidad ofrecida recibe un precio superior al que estaría dispuesto a percibir. Dicha zona delimita gráficamente el excedente del productor.
Autor: bolgspot
RESUMEN: La unidad 3 trata sobre la integral definida, así como el área bajo la curva y el teorema fundamental de cálculo.
BIBLIOGRAFIAS:
hyperphysics. (2012). Área Bajo una Curva. 2012, de http://hyperphysics.phy-astr.gsu.edu/ Sitio web: http://hyperphysics.phy-astr.gsu.edu/hbasees/integ.html
cetremo14. (Publicado el 9 mar. 2012). Cálculo Integral - Tutorial de Área bajo la curva. el 9 mar. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=5vY4vML5wTw
WIKIPEDIA. (el 17 nov 2015 a las 09:43.). Teorema fundamental del cálculo. 17 nov 2015 a las 09:43, de wikipedia Sitio web: https://es.wikipedia.org/wiki/Teorema_fundamental_del_c%C3%A1lculo
Me Salva!. (Publicado el 7 may. 2014). Me Salva! INT14 - Teorema fundamental do cálculo. el 7 may. 2014, de youtube Sitio web: https://www.youtube.com/watch?v=igeUS5PytV4
VITUTOR. (2012). Integral definida. 2012, de vitutor Sitio web: http://www.vitutor.com/integrales/definidas/integral_definida.html
Academatica. (Subido el 15 mar. 2011). Propiedades de la integral definida. el 15 mar. 2011, de youtube Sitio web: https://www.youtube.com/watch?v=QwAgIWikGwk
Inetor. (2012). Área comprendida entre dos funciones. 2012, de inetor Sitio web: http://www.inetor.com/definidas/integral_area2.html
unicoos. (Subido el 7 ene. 2012). Area entre funciones 02 BACHILLERATO integral definida. el 7 ene. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=XYV2NpMZB44
Matemáticas II. (miércoles, 26 de noviembre de 2014). aplicaciones: Excedente del Consumidor y del Productor, valor presente y valor futuro. miércoles, 26 de noviembre de 2014, de blogger Sitio web: http://matematicas2jairoreyes.blogspot.mx/2014/11/35-aplicaciones-excedente-del.html
Efrain Nava Alvarez. (Publicado el 6 abr. 2012). Excedente o superávit del consumidor y del productor con Geogebra. el 6 abr. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=66YeIjunXJ0
BIBLIOGRAFIAS:
hyperphysics. (2012). Área Bajo una Curva. 2012, de http://hyperphysics.phy-astr.gsu.edu/ Sitio web: http://hyperphysics.phy-astr.gsu.edu/hbasees/integ.html
cetremo14. (Publicado el 9 mar. 2012). Cálculo Integral - Tutorial de Área bajo la curva. el 9 mar. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=5vY4vML5wTw
WIKIPEDIA. (el 17 nov 2015 a las 09:43.). Teorema fundamental del cálculo. 17 nov 2015 a las 09:43, de wikipedia Sitio web: https://es.wikipedia.org/wiki/Teorema_fundamental_del_c%C3%A1lculo
Me Salva!. (Publicado el 7 may. 2014). Me Salva! INT14 - Teorema fundamental do cálculo. el 7 may. 2014, de youtube Sitio web: https://www.youtube.com/watch?v=igeUS5PytV4
VITUTOR. (2012). Integral definida. 2012, de vitutor Sitio web: http://www.vitutor.com/integrales/definidas/integral_definida.html
Academatica. (Subido el 15 mar. 2011). Propiedades de la integral definida. el 15 mar. 2011, de youtube Sitio web: https://www.youtube.com/watch?v=QwAgIWikGwk
Inetor. (2012). Área comprendida entre dos funciones. 2012, de inetor Sitio web: http://www.inetor.com/definidas/integral_area2.html
unicoos. (Subido el 7 ene. 2012). Area entre funciones 02 BACHILLERATO integral definida. el 7 ene. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=XYV2NpMZB44
Matemáticas II. (miércoles, 26 de noviembre de 2014). aplicaciones: Excedente del Consumidor y del Productor, valor presente y valor futuro. miércoles, 26 de noviembre de 2014, de blogger Sitio web: http://matematicas2jairoreyes.blogspot.mx/2014/11/35-aplicaciones-excedente-del.html
Efrain Nava Alvarez. (Publicado el 6 abr. 2012). Excedente o superávit del consumidor y del productor con Geogebra. el 6 abr. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=66YeIjunXJ0

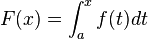



![m \leq f(x) \leq M \; \forall x \in [a,b]](https://upload.wikimedia.org/math/1/e/1/1e1b2ad811ce2c15f191c634ded2afd9.png)





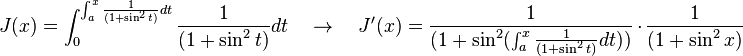
![\exists \xi\in[a,x]
: \quad
f(\xi)=
\frac{1}{x-a}\int_{a}^{x}f(t)dt](https://upload.wikimedia.org/math/f/c/c/fcc1b09852259ebc9a49ff937d0fe4ca.png)





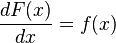


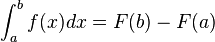
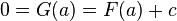

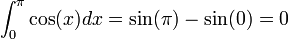
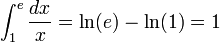

 .
.



































