Objetivo: El alumno
comprenderá los conceptos básicos del cálculo diferencial en varias variables,
así como la resolución de problemas en el entorno económico-administrativo,
enfatizando aquellos del área de optimización de recursos.
1.1 Funciones En Dos Variables
Una función de dos variables es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y sólo un número real z.
El conjunto de parejas ordenadas para las cuales la regla de correspondencia da un número real se llama dominio de la función. El conjunto de valores z que corresponden a los pares ordenados se llama imagen o contra dominio.
Una función de dos variables se denota usualmente con la notación
z = f (x, y)
Las variables x, y se llaman variables independientes, y z se llama variable dependiente.
La gráfica de una función de dos variables es el conjunto de puntos con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).
Este conjunto de puntos forma una superficie en el espacio tridimensional.


En consecuencia, la gráfica de una función f de dos variables es una superficie que consta de todos los puntos del espacio tridimensional cuyas coordenadas cartesianas están determinadas por las ternas ordenadas de números reales (x, y, z). Como el dominio de f es un conjunto de puntos del plano x, y, y puesto que cada par ordenado (x, y) del dominio de f corresponde a solo un valor de z, ninguna recta perpendicular al plano x,y puede interceptar a la gráfica de f en mas de un punto.
Ejemplo ilustrativo 1
La función f del ejemplo 1 es el conjunto de todos los pares ordenados de la forma (P, z) tales que
 z=v25- x2 -y2
z=v25- x2 -y2
Por tanto, la gráfica de f es la semiesfera en el plano x y por arriba de este cuyo centro es el origen y tiene radio 5. Esta semiesfera se muestra en la figura 1.

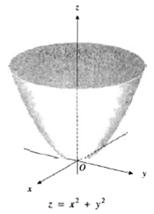
Ejemplo 2: dibuje la gráfica de la función
Sol/: la gráfica de f es la superficie que tiene la ecuación z=x2 +y2 . La traza de la superficie en el plano x,y se obtiene al utilizar la ecuación z=0 simultáneamente con la ecuación de la superficie. Al hacerlo resulta x2 +y2=0 la cual representa el origen. Las trazas en los planos xz y yz se obtiene al emplear las ecuaciones z=x2 +y2. Estos trazos son las parábolas z= x2y z= y2.
Autor: Monografias
http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml
1.2 Derivadas Parciales
Autor: Wikipedia
https://es.wikipedia.org/wiki/Derivada_parcial
1.3 Máximos y Mínimos de Funciones de Dos Variables
 ;
;


 Ejemplo:
Ejemplo:
 ;
;




Autor: Matap
http://www.matap.uma.es/~svera/probres/pr3/pr3a3_1.html#extremos
1.4 Aplicaciones: Optimización de Funciones de Dos Variables que Representen Gastos, Ingresos o Utilidad








http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml
1.2 Derivadas Parciales
En matemática, una derivada parcial de una función de diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en cálculo vectorial y geometría diferencial.
La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:
Donde  es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
 es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
Cuando una magnitud  es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,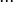 ), es decir:
), es decir:
 es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
, ), es decir:
), es decir:
Al realizar esta derivada obtenemos la expresión que nos permite obtener la pendiente de la recta tangente a dicha función en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
 en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.
Ejemplos:
- Considera el volumen V de un cono, este depende de la altura h del cono y su radio r de acuerdo con la fórmula
Las derivadas parciales de V respecto a r y h son:
- Otro ejemplo, dada la función
 tal que:
tal que:
la derivada parcial de  respecto de
respecto de  es:
es:
 respecto de
respecto de  es:
es:
mientras que con respecto de  es:
es:
 es:
es:Autor: Wikipedia
https://es.wikipedia.org/wiki/Derivada_parcial
1.3 Máximos y Mínimos de Funciones de Dos Variables
Definición. Una función  tiene un máximo (mínimo) en un punto
tiene un máximo (mínimo) en un punto  si el valor de la función en este punto es mayor (menor) que su valor en cualquier otro punto X(x,y) de algún entono de P.
si el valor de la función en este punto es mayor (menor) que su valor en cualquier otro punto X(x,y) de algún entono de P.
Condiciones necesarias de extremo.
Si una función diferenciable  alcanza un extremo en el punto
alcanza un extremo en el punto  entonces sus derivadas parciales de primer orden en este punto son iguales a cero, o sea:
entonces sus derivadas parciales de primer orden en este punto son iguales a cero, o sea:
Los puntos en los que las derivadas parciales son iguales a cero se llaman puntos críticos o estacionarios. No todo punto crítico es un punto extremo.
Condiciones suficientes para la existencia de extremos.
(a) Caso de dos variables. Sea  un punto crítico de una función
un punto crítico de una función  con las derivadas parciales de segundo orden continuas en P, y sea
con las derivadas parciales de segundo orden continuas en P, y sea el determinante de su matriz hessiana, entonces:
el determinante de su matriz hessiana, entonces:


Es decir, si el hessiano es positivo hay extremo (el tipo nos lo da  , si es negativa máximo y si es positiva mínimo). Si el hessiano es negativo no hay extremo. Y si el hessiano es cero hay duda (que habrá que resolver por otro método)
, si es negativa máximo y si es positiva mínimo). Si el hessiano es negativo no hay extremo. Y si el hessiano es cero hay duda (que habrá que resolver por otro método)
Halla los extremos de la función 
Solución:
(a) Calculamos las derivadas parciales de primer orden.
Los puntos críticos se obtienen igualando a cero las derivadas parciales.
y resolviendo el sistema obtenemos x=0, y=3. Luego P(0,3) es el único punto crítico de la función.
Hallamos la matriz hessiana de f en P(0,3).

Con lo cual tenemos H(0,3)=+3 luego hay extremo y como  se trata de un mínimo.
se trata de un mínimo.
El valor de la función en el mínimo es f(0,3)=-8.
Autor: Matap
http://www.matap.uma.es/~svera/probres/pr3/pr3a3_1.html#extremos
1.4 Aplicaciones: Optimización de Funciones de Dos Variables que Representen Gastos, Ingresos o Utilidad
Problemas de optimización
Los métodos para hallar valores extremos que hemos aprendido tienen aplicaciones practicas en muchas áreas de nuestra vida. Una persona de negocios quiere minimizar los costos y maximizar las utilidades. El principio de Fermat, en óptica, afirma que la luz sigue la trayectoria que recorre en el menor tiempo. Lo que en algunos casos se conoce como la linea recta. En esta sección trataremos de resolver problemas como lo de maximizar áreas, volúmenes y utilidades, minimizar distancias, tiempos y costos.
En la solución de problemas prácticos, el desafió mas grande suele ser convertir el problema en palabras en un problema matemático de optimización, establecer la función que debe maximizarse o minimizarse. Recuerdo los principios de solución de problemas.
#Comprenda el problema.#Analogía : Intente casos especiales.#Dibuje Diagramas.
Pasos para la solución de problemas de optimizan
- COMPRENDA EL PROBLEMA: El primer paso, es leer el problema con cuidado hasta que se entienda con claridad. Hágase preguntas como: Cual es la incógnita?, ¿Cuáles son las cantidades dadas?, ¿Cuáles son las condiciones dadas?.
- DIBUJE UN DIAGRAMA DEL PROBLEMA: En la mayor parte de los problemas, resulta útil dibujar un diagrama e identificar en el las cantidades dadas requeridas.
- INTRODUZCA NOTACIÓN: Asigne un símbolo a la cantidad que se va a maximizar o minimizar. Por ejemplo V = volumen, h = altura, b = base etc.
- Escriba una fórmula para la función objetivo Q que se maximizará o minimizará, en términos de las variables.
- Utilice las condiciones del problema para eliminar todas, excepto una de esta variables, y por consiguiente expresar Q como una función de una sola variable.
- DERIVAR
- IGUALAR LA DERIVADA: A cero para encontrar los puntos críticos.
- SEGUNDA DERIVADA: Deducir con la prueba de la segunda derivada si los puntos críticos son máximos o mínimos.
- DAR LA SOLUCIÓN: Recuerda dar una solución clara de su problema en notación Ingenieril.
Otra Forma de verlo
- . Se plantea la función que hay que maximizar o minimizar.
- . Se plantea una ecuación que relacione las distintas variables del problema, en el caso de que haya más de una variable.
- .Se despeja una variable de la ecuación y se sustituye en la función de modo que nos quede una sola variable.
- . Se deriva la función y se iguala a cero, para hallar los extremos locales.
- . Se realiza la 2ª derivada para comprobar el resultado obtenido.
Tip:
Use siempre su intuición para obtener alguna idea de cuál debe de ser la solución correcta del problema. Para muchos problemas físicos puede tener una estimación aproximada del valor óptimo antes de que comience a realizar los detalles, lo cual lo guiará de forma mas fácil durante la resolución del mismo.
1Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 12 cm.
Autor: Wikimatematica
Ejemplos:1Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 12 cm.
2 Hallar las dimensiones que hacen mínimo el coste de un contenedor que tiene forma de paralelepípedo rectangular sabiendo que su volumen ha de ser 9 m3 , su altura 1 m y el coste de su construcción por m2 es de 50 € para la base; 60 para la etapa y 40 para cada pared lateral.








Autor: Vitutor
RESUMEN: La unidad 1 trata sobre las funciones de dos variables, así como sus máximos y mínimos y su aplicación en problemas económico-administrativo.
BIBLIOGRAFIAS:
Monografias.com. (2011). Funciones de dos y más variables, dominio y rango, y curva de nivel Leer más: http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml#ixzz3sHUY2dJj. 2011, de monografias.com Sitio web: http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml
Academatica. (Publicado el 12 ene. 2013). Video de funciones de dos variables - introducción. el 12 ene. 2013, de youtube Sitio web: https://www.youtube.com/watch?v=9FpkWkqCDV0
Wikipedia. (el 16 jul 2014 a las 21:49.). Derivada parcial. el 16 jul 2014 a las 21:49., de wikipedia Sitio web: https://es.wikipedia.org/wiki/Derivada_parcial
unicoos. (Subido el 9 feb. 2012). Vector Gradiente UNIVERSIDAD unicoos matematicas derivadas parciales. el 9 feb. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=hQjPW5hsU2o
Salvador Vera. (2010). xtremos de una función de varias variables. . 2010, de matap Sitio web: http://www.matap.uma.es/~svera/probres/pr3/pr3a3_1.html#extremos
Wikimatematica. (el 11 abr 2012, a las 19:03.). Problemas de optimizacion. el 11 abr 2012, a las 19:03., de wikimatematica.org Sitio web: http://www.wikimatematica.org/index.php?title=Problemas_de_optimizacion
Vitutor. (2012). optimizacion de funciones. 2012, de vitutor Sitio web: http://www.vitutor.com/fun/5/b_a.html
BIBLIOGRAFIAS:
Monografias.com. (2011). Funciones de dos y más variables, dominio y rango, y curva de nivel Leer más: http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml#ixzz3sHUY2dJj. 2011, de monografias.com Sitio web: http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml
Academatica. (Publicado el 12 ene. 2013). Video de funciones de dos variables - introducción. el 12 ene. 2013, de youtube Sitio web: https://www.youtube.com/watch?v=9FpkWkqCDV0
Wikipedia. (el 16 jul 2014 a las 21:49.). Derivada parcial. el 16 jul 2014 a las 21:49., de wikipedia Sitio web: https://es.wikipedia.org/wiki/Derivada_parcial
unicoos. (Subido el 9 feb. 2012). Vector Gradiente UNIVERSIDAD unicoos matematicas derivadas parciales. el 9 feb. 2012, de youtube Sitio web: https://www.youtube.com/watch?v=hQjPW5hsU2o
Salvador Vera. (2010). xtremos de una función de varias variables. . 2010, de matap Sitio web: http://www.matap.uma.es/~svera/probres/pr3/pr3a3_1.html#extremos
Wikimatematica. (el 11 abr 2012, a las 19:03.). Problemas de optimizacion. el 11 abr 2012, a las 19:03., de wikimatematica.org Sitio web: http://www.wikimatematica.org/index.php?title=Problemas_de_optimizacion
Vitutor. (2012). optimizacion de funciones. 2012, de vitutor Sitio web: http://www.vitutor.com/fun/5/b_a.html

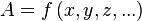

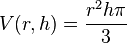
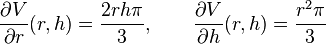

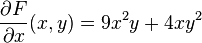
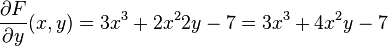











No hay comentarios:
Publicar un comentario